7 Elektronische Bauelemente im Gleichstromkreis

7.2 Die Spule

Im Jahr 1802 entdeckte der italienische Jurist und Philosoph Gian Domenico Romagnosi (1761–1835), der zugleich Hobbyphysiker war, die ablenkende Kraft des elektrischen Stromes auf eine Kompassnadel. Seine Veröffentlichung wurde jedoch nicht beachtet und geriet daher in Vergessenheit. Erst 18 Jahre später entdeckte auch Hans Christian Ørsted (1777–1851) die magnetische Kraftwirkung eines stromdurchflossenden Leiters.

Die Erarbeitung der theoretischen Grundlagen zu diesem Phänomen, machte die Entwicklung elektrischer Antriebe, Sende- und Empfangsanlagen moderner Kommunikationsmittel, Energieübertragungen über große Distanzen, Induktionsherde für Industrie und Haushalt, Frequenzweichen in Lautsprecherboxen und viele andere technische Errungenschaften erst möglich.

 

7.2.1 Magnetismus und seine Ursachen

Die Entstehung des magnetischen Feldes resultiert aus zwei unterschiedlichen Bewegungen der Elementarladungen (Elektronen). Einerseits bewegen sich die Elektronen um die Atomkerne, andererseits dreht sich jedes Elektron mit sehr hoher Geschwindigkeit um seine eigene Achse (Elektronenspin). Beide Bewegungsarten sind voneinander unabhängig und verursachen unterschiedliche Magnetfelder (Bild 20).

Die Bahnbewegung stellt einen sehr kleinen geschlossenes Stromkreis dar, in dem lediglich die Elementarladung transportiert wird. Das daraus resultierende magnetische Feld wird – wie beim elektrischen Feld des Kondensators – mit Hilfe von Feldlinien dargestellt. Diese sind kreisförmig und verlaufen senkrecht zur Bahnbewegung. Die Einzelfelder ergänzen sich zu einem Gesamtfeld, welches die Bewegungsebene von unten nach oben „durchflutet“ (lange grüne Feldlinien).

Die magnetischen Felder der Elektronenbahnen in einem leitfähigen Material treten nach Außen nicht in Erscheinung, da sie sich durch die ungeordneten und zufälligen Bewegungsrichtungen der Elektronenbahnen gegenseitig kompensieren. Auch können die Elektronenbahnen nicht so beeinflusst werden, dass ein gerichtetes Gesamtfeld mit starken magnetischen Eigenschaften entsteht.

Anders sieht es jedoch beim Elektronenspin aus. Die Eigenrotation des Elektrons stellt eine Miniaturbahnbewegung mit einem sehr kleinen Radius dar. Auch bei dieser Bewegung verlaufen die Feldlinien senkrecht zur Rotationsbewegung, also in Richtung der Rotationsachse. Die fortwährende Rotation mit der gleichen Drehgeschwindigkeit und -richtung sorgt jedoch für eine Lagestabilisierung des Elektrons (Kreisel-Effekt). Dadurch stellt sich für jedes Elektron ein kleines stabiles magnetisches Feld mit gleichbleibender Feldlinienrichtung ein. Da das Elektron die kleinste elektrische Ladung darstellt, bezeichnet man die magnetische Wirkung des Elektronenspins auch als Elementarmagnet. Die gerichtete Elektronenbewegung in einem Leiter verursacht eine einheitliche Ausrichtung von Elektronen-Spinachsen. Infolgedessen summieren sich die Magnetfelder der Elementarmagnete zu einem Gesamtfeld, welches sich um den Leiter herum ausbildet.

 

7.2.2 Magnetfeld eines stromdurchflossenen Leiters

Bei einem Stromfluss durch einen kreisförmigen Leiter, entstehen konzentrische Feldlinien um den Leiter (Bild 21). Fließt ein Strom in den Leiter hinein, verlaufen die Feldlinien im Uhrzeigersinn. Wird die Stromrichtung umgekehrt, ändert sich die Richtung der Feldlinien. Die technische Stromrichtung wird mit einem Kreuz (X) oder einem Punkt (•) auf der Querschnittsfläche des Leiters gekennzeichnet. Das Kreuz symbolisiert die Rückansicht des Strompfeiles, der vom Betrachter weg in den Leiter hinein zeigt. Der Punkt symbolisiert die Spitze des Strompfeiles. Er zeigt auf den Betrachter.

Der Feldlinienverlauf bei der technischen Stromrichtung kann sehr gut mit den Bewegungsrichtungen eines Korkenziehers verglichen werden (Bild 22). Die Drehrichtung des Korkenziehers symbolisiert die Richtung der magnetischen Feldlinien. Die damit einhergehende horizontale Bewegung des Korkenziehers (in oder aus dem Korken heraus) gibt die Richtung des Stromes an.

Mit der Korkenzieherregel lässt sich somit auf einfache Weise bei gegebener Feldlinienrichtung die Richtung des Stromes oder bei gegebener Stromrichtung die Richtung der Feldlinien bestimmen.

Die magnetische Kraft bzw. Stärke des Feldes ist von der Höhe des fließenden Stromes und vom Abstand zum Leiter abhängig.

Die magnetische Feldstärke ist dem Strom direkt proportional. Mit einer Stromzange (siehe 4.6.1 Strommessung) lässt sich daher indirekt über eine Messung des magnetischen Feldes der Strom durch einen Leiter bestimmen. Ein Auftrennen des Stromkreises ist nicht erforderlich.

 

7.2.3 Magnetische Kraftwirkungen paralleler stromdurchflossener Leiter

Werden zwei in kleinem Abstand parallel liegende Leiter von einem hohen Strom durchflossen, üben die um die Leiter entstehenden Magnetfelder Kräfte aufeinander aus. Unter der Internetadresse

http://www.youtube.com/watch?v=43AeuDvWc0k

können Sie die Kraftwirkungen auf die Leiter in einem Video sehen. Es zeigt, dass bei Parallelschaltung der Leiter (gleiche Stromrichtungen), eine gegenseitige Anziehung erfolgt. Werden die Leiter hingegen in Serie geschaltet (gegensätzliche Stromrichtungen), kommt es zu einer Abstoßung der Leiter.

Die Grafiken in Bild 23 verdeutlichen die Kraftwirkungen auf die Leiter mit Hilfe der magnetischen Feldlinien. Bei gleicher Stromrichtung überlagern sich die einzelnen Magnetfelder zu einem Gesamtmagnetfeld, das beide Leiter umschließt und somit anzieht. Werden die Leiter gegensinnig vom Strom durchflossen, entsteht zwischen den Leitern eine Feldlinienverdichtung mit abstoßender Wirkung.

 

7.2.4 Magnetfeldbündelung durch Drahtwicklungen – der Aufbau einer Zylinderspule

Je größer die Zahl der nebeneinander liegenden und gleichsinnig vom Strom durchflossenen Leiter ist, desto stärker ist das die Leiter umschließende magnetische Feld.

Wird ein langer isolierter Leiterdraht immer in der gleichen Richtung z. B. auf einen zylindrischen hohlen Kunststoffkörper gewickelt, so entsteht eine Luftspule mit einem magnetischen Gesamtfeld. In Bild 24 ist der Längsschnitt einer zylindrischen Luftspule zu sehen, die zehn Windungen besitzt. Innerhalb der Spule tritt eine hohe Feldliniendichte bei einem nahezu parallelen (homogenen) Feldlinienverlauf auf. Außerhalb der Spule nimmt die Feldliniendichte mit größerer Entfernung von der Spule ab. Aufgrund des im Uhrzeigersinn fließenden Spulenstromes treten die Feldlinien auf der linken Seite aus und auf der rechten Seite wieder in die Spule ein. Das Magnetfeld der Spule ist mit dem eines Stabmagneten vergleichbar. Dort wo die Feldlinien die Spule verlassen, bildet sich ein magnetischer Nordpol; dort wo sie in die Spule eindringen, ein Südpol.

Die Spule stellt somit ein Magnet dar, der sich elektrisch ein- und ausschalten lässt (Elektromagnet). Allerdings ist für die Ausbildung eines starken Magnetfeldes in der Luftspule ein relativ hoher Strom notwendig, der mit einem größeren Querschnitt für den Wickeldraht (Vermeidung einer unzulässigen Erwärmung der Wicklung) verbunden ist.

Ein großer Leiterquerschnitt hat aber den Nachteil, dass die Baugröße einer Spule bei gleicher Windungszahl stark zunimmt. Es stellt sich somit die Frage, durch welche anderen Größen die Stärke des Magnetfeldes beeinflusst werden kann.

 

7.2.5 Die magnetischen Grundgrößen

Aus dem letzten Abschnitt ist Ihnen bekannt, dass die magnetische Kraftwirkung um einen geraden Leiter mit Hilfe der magnetischen Feldstärke H (magnetische Kraft) berechnet werden kann (Gleichung {7.2.1}). In diesem Abschnitt soll ermittelt werden, welche Größen die magnetische Feldstärke einer zylindrischen Luftspule beeinflussen.

Für die Messung des Kraftfeldes benötigen wir – neben der Spule, der Spannungsquelle und einem Vorwiderstand – einen Stabmagneten und eine einfache Federwaage. In Bild 25 ist der Versuchsaufbau dargestellt. Als Spannungsquelle wird ein 12 V Blei-Akkumulatur mit einer Ladungsmenge von Q = 1,3 Ah vom Hersteller Ultracell^© verwendet.

Vermeiden Sie unter allen Umständen einen Kurzschluss des Akkus! Der Strom wird dann sehr groß und wenn Sie für Ihre Zuleitung einen kleinen Leiterquerschnitt verwenden, schmilzt die Isolierung und setzt gesundheitsschädliche Gase frei.

Zur Übung können Sie einmal den Kurzschlussstrom unter der Voraussetzung ausrechnen, dass Sie mit einer 1 m langen Telefonleitung (A = 0,6 mm²) den Kurzschluss verursachen und der Innenwiderstand des 12 V Akkus 0,9 Ω beträgt.

Zunächst soll der Zusammenhang zwischen dem Strom und der magnetischen Kraft bei konstanter Windungszahl ermittelt werden. Dabei untersuchen wir die Eigenschaften einer realen Spule. Diese besteht aus einem lackisolierten Kupferdraht mit konstanten Querschnitt und einer festen Länge. Die Drahtlänge ist vom Durchmesser des gewählten Spulenkörpers und der Zahl der Windungen abhängig. Damit besitzt der aufgewickelte Kupferdraht bei konstanter Temperatur einen festen Widerstandswert R_L (siehe auch: 4.5.7 Widerstand eines Leiters).

Die im Versuchsaufbau verwendete Spule hat einen Drahtwiderstand von R_L = 20 Ω.

Schließen wir die Spule direkt an die Spannungsquelle an, fließt ein Strom von 0,6 A. Dieser Strom erzeugt eine magnetische Kraft, die mit Hilfe der Federwaage abgelesen werden kann (Bild 25, links). Für die zweite Messung wird ein Vorwiderstand^* in die Schaltung eingefügt, dessen Widerstandswert genauso groß wie der Spulenwiderstand ist (Bild 25, rechts). Auf diese Weise verringert sich der Spulenstrom auf die Hälfte des ursprünglichen Wertes (0,3 A). Die Spannung an der Spule sinkt auf 6 V ab, weil sich die Gesamtspannung auf die beiden gleich großen Widerstände R_V und R_L aufteilt. Die magnetische Zugkraft an der Federwaage ist nur noch halb so groß.

^*Bitte beachten Sie, dass der verwendete Vorwiderstand eine ausreichende Verlustleistung besitzen muss. Hat er eine zu kleine Verlustleistung (Bauform), kann er u. U. sehr heiß werden. Mit Ihren bisher erlernten Elektrotechnik-Kenntnissen sollten Sie die notwendige Verlustleistung berechnen können (siehe 6.2.1 Maximale Verlustleistung von Bauelementen).

Als Nächstes soll untersucht werden, wie sich die Änderung der Windungszahl auf die magnetische Kraft bei einem konstant gehaltenden Strom auswirkt (Bild 26). Damit der Strom unverändert bleibt, darf sich der Gesamtwiderstand der beiden Schaltungen nicht verändern.

Im Bild 26, rechts, wurde die Windungszahl der Spule halbiert. Da eine Reduzierung der Windungszahl mit der Verkleinerung des Spuleninnenwiderstandes verbunden ist, muss der verloren gegangene Wicklungswiderstand von annähernd 10 Ω durch einen ebenso großen, in Reihe zur Spule geschalteten Widerstand, ergänzt werden.

Die Spulenwicklung besteht aufgrund der hohen Windungszahl aus mehren Lagen. Damit besitzt die äußere Lage einen größeren Durchmesser als die innere. Bei einer Halbierung der Windungszahl verringert sich die Länge des Wicklungsdrahtes daher auf weniger als die Hälfte des ursprünglichen Wertes. Das Gleiche gilt für den Wicklungswiderstand. Um den Strom exakt einstellen zu können wird daher ein 22 Ω-Potentiometer (mit ausreichend großer Verlustleistung!) verwendet.

Aus der Versuchsanordnung ergibt sich, dass die magnetische Kraft auf den halben Wert absinkt, wenn die Windungszahl halbiert wird.

Im nächsten Schritt soll geprüft werden, ob die Baulänge des Spulenkörpers einen Einfluss auf die magnetische Kraft hat.

In Bild 27 sind zwei Spulen dargestellt, die gleiche Windungszahlen aber unterschiedlich lange Spulenkörper besitzen. Die rechte Spule hat im Vergleich zur linken einen doppelt so langen Spulenkörper. Die Zahl der Windungen und die Höhe des Stromes ist bei beiden Spulen identisch.

Das Magnetfeld der längeren Spule ist weniger stark. Es erzeugt eine magnetische Kraft, die nur halb so groß, wie die der linken Spule ist. Eine kürzere Spulenlänge bewirkt – bedingt durch die dichtere Spulenwicklung und der damit einhergehenden stärkeren Konzentration der Feldlinien – eine höhere magnetische Kraftwirkung.

Die drei Teilergebnisse unser vorhergehenden Betrachtungen können in einer Gleichung zusammengefasst werden.

Ist die Spule nicht zylindrisch sondern ringförmig gewickelt, können die Feldlinien aus der Spule nicht austreten (Bild 28). Es entsteht eine Ringspule mit homogenen Magnetfeld und die Feldlinien verlaufen konzentrisch. Da die Länge der Feldlinie mit größerem Abstand vom Zentrum steigt, wird für die Berechnung der durchschnittlichen magnetischen Feldstärke die mittlere Feldlinienlänge l_m verwendet.

 

Die magnetische Wirkung einer Spule lässt sich erheblich steigern, wenn in den Spulenhohlraum ein massives zylindrisches Eisenstück eingeführt wird. Im Bild 29 ist die Menge der angezogenen Stahlnägel einer Spule ohne und mit Eisenkern zu sehen. Jedes im Spulenkörper befindliche Medium wird von den Feldlinien durchdrungen. Da bei konstanter Feldstärke und Feldlinienzahl die Stoffe Luft und Eisen sehr unterschiedlich Kraftwirkungen verursachen, scheint jeder Stoff einen bestimmten magnetischen Widerstand zu verursachen. Der magnetische Widerstand von Eisen ist geringer als der von Luft oder anders formuliert, die magnetische Leitfähigkeit des Eisens ist höher. Durch die Magnetfeld verstärkende Wirkung des Kernmaterials entsteht ein starker Elektromagnet.

Die verstärkende Wirkung beruht darauf, dass bestimmte Materialien ihre Elementarmagnete unter dem Einfluss magnetischer Fremdfelder ausrichten und damit selbst zu einem Magneten werden. Zu ihnen gehören Eisen, Kobalt und Nickel. Sie sind „ferromagnetisch“. Aufgrund dieser Eigenschaft, besitzen sie eine gute magnetische Leitfähigkeit. Die Leitfähigkeit ist allerdings stark von der Stärke des äußeren Magnetfeldes abhängig.

Die Veränderung der magnetischen Leitfähigkeit durch bestimmte Stoffe wird mit Hilfe der magnetischen Permeabilität µ beschrieben. Sie ist vergleichbar mit der Permittivität des Kondensators. Als Maßstab dient auch hier der materiefreie Raum – das Vakuum. Im Vakuum ist die Permeabilität eine konstante Größe. Der absolute Wert dieser Größe wird absolute Permeabilität oder magnetische Feldkonstante µ₀ genannt.

Eine höhere magnetische Leitfähigkeit führt zu einer Verdichtung der Feldlinien und somit zu einer Konzentration des magnetischen Feldes innerhalb des in die Spule eingebrachten Stoffes. Die höhere Feldliniendichte erzeugt eine größere magnetische Kraft. In Bild 30 ist dieser Effekt anhand eines Hufeisenmagneten dargestellt, in deren Mitte sich ein Eisenstück befindet.

Die Leitfähigkeit bzw. die Feldliniendichte kann bei bestimmten Materialien aber auch abnehmen. Die materialspezifische Feldliniendichte ist somit vergleichbar mit der Höhe des Stromes durch einen Leiter, dessen spezifische Leitfähigkeit von der Art des Materials abhängig ist. Wird als Leitermaterial (bei gleicher Versorgungsspannung sowie Querschnitt, Länge und Temperatur des Leiters) statt Kupfer, Aluminium verwendet, sinkt der Strom und somit die elektrische Leitfähigkeit. Im Vergleich dazu vergrößert sich der Strom bei Verwendung von Silber, weil dessen elektrische Leitfähigkeit höher als die von Kupfer ist.

Das Produkt aus der magnetischer Feldstärke und der Permeabiltät macht eine Aussage über die Feldliniendichte. Sie wird magnetische Flussdichte B oder magnetische Induktion genannt.

In Bezug auf die magnetische Permeabilität werden drei Materialarten unterschieden, deren Magnetisierungskennlinien in Bild 31 (nicht maßstabsgerecht) zu sehen sind. Neben den bereits genannten ferromagnetischen Stoffen, gibt es paramagnetische und diamagnetische Stoffe.

Die Permeabilitäten (spezifische Leitfähigkeiten) ferromagnetischer Stoffe (Eisen, Kobalt und Nickel) haben einen nichtlinearen Verlauf, sind also stark von der magnetischen Feldstärke H abhängig (rote Kennlinie). Anhand der in Bild 31 dargestellten Tangenten ist zu erkennen, dass zu Beginn die Kennlinie sehr flach verläuft (1). Die Permeabilitätszahl µ_r ist sehr klein. Bei einer bestimmten Feldstärke erreicht die Permeabilitätszahl den größten Wert (größte Steigung) und führt somit zu einem starken Anstieg der magnetischen Flussdichte B (2). Mit weiter zunehmender Feldstärke nimmt die Steigung der Tangente und somit der Wert der Permeabilitätszahl wieder ab (3). Danach führt eine weitere Erhöhung der Feldstärke nur noch zu einem sehr geringen Anstieg der magnetischen Flussdichte. Die Permeabilitätszahl sinkt auf einen kleinen Wert ab (4).

Da sich die Magnetisierungskennlinien bei ferromagnetischen Stoffen mathematisch nicht erfassen lassen, ermitteln die Hersteller die Kennlinien messtechnisch und stellen sie anschließend ihren Kunden zur Verfügung. Mit den materialspezifischen Magnetisierungskennlinien (oder alternativ Wertetabellen) und der nach µ_r umgestellten Gleichung {7.2.8} der magnetische Flussdichte, lässt sich für eine beliebige Feldstärke H der Wert der Permeabilitätszahl µ_r bestimmen.

Unter dem nachfolgenden Link finden Sie Magnetisierungskennlinien des schweizer Herstellers Karl Schupp AG.

http://www.schupp.ch/de/katalog_de_pdf/SK_05_Kennlinien.pdf

Ferromagnetische Stoffe besitzen sehr hohe Permeabilitätszahlen und werden deshalb mit großer Kraft in ein Magnetfeld hineingezogen. Sie verlieren ihre magnetischen Eigenschaften, wenn Sie auf ihre Curie-Temperatur (Eisen ca. 800 °C) erwärmt oder starken mechanischen Erschütterungen ausgesetzt werden.

Paramagnetische Stoffe (Chrom, Aluminium, Sauerstoff) besitzen eine konstante Permeabilitätszahl, die nur etwas größer als die des Vakuums ist (µ_r > 1, grüne Kennlinie in Bild 31). Sie werden daher von Magnetfeldern leicht angezogen. Der Sauerstoff (CO₂) hat im Vergleich zu anderen Gasen die stärksten paramagnetischen Eigenschaften. Mit Hilfe eines magnetischen Feldes ist es daher möglich, die Sauerstoffkonzentration in Abgasen zu messen und z. B. die Effektivität der Verbrennung eines Benzin- oder Diesel-Motors zu ermitteln. Des Weiteren werden paramagnetische Materialien für den exakten Abgleich von Schwingkreis-Spulen in der Hochfrequenztechnik benutzt.

Diamagnetische Stoffe (Kupfer, Wismut, Wasser) haben eine konstante Permeabilitätszahl, die nur geringfügig kleiner als die des Vakuums ist (µ_r < 1, blaue Kennlinie in Bild 31). Dadurch kommt es zu einer geringfügigen Abstoßung des Materials durch ein äußeres magnetische Feld. Die diamagnetischen Eigenschaften von Wasser können – allerdings nur unter extrem starken Magnetfeldern – dazu genutzt werden, um wasserreiche Objekte zum Schweben zu bringen.

In den nachfolgenden Tabellen sind die Permeabilitätszahlen der unterschiedlichen Stoffgruppen aufgelistet. Bei den ferromagnetischen Stoffen wird von den Herstellern in der Regel die Anfangspermeabilitätszahl µ_r, a (Amplitudenpermeabilität) bei einer Feldstärke, die gegen den Wert Null strebt (H → 0) angegeben oder die Permeabilitätzahl bei einer magnetischen Feldstärke von H = 4 mA/cm (µ_r, 4).

Permeabilitätszahlen ferromagnetischer Werkstoffe (µr >> 1)
	Anfangspermeabilität µr, a	Maximalpermeabilität µr, max
Elektrolyt-Eisen	600	15 000
Ferrite	300 bis 3 000
Gusseisen	70	600
Nickel-Eisen-Legierung	2 700	20 000
Reinstes Eisen	25 000	250 000
Stahl mit 1 % Kohlenstoff	40	7 000
Supermalloy (Legierung)	100 000	300 000
Technisches Eisen	250	7 000
Transformatorenblech	600	7 600

 

Permeabilitätszahlen paramagnetischer (µr > 1) und diamagnetischer Stoffe (µr < 1)
paramagnetische Stoffe		diamagnetische Stoffe
Sauerstoff	1,000 000 3	Wasser	0,999 991
Luft	1,000 000 4	Kupfer	0,999 990
Zinn	1,000 003 8	Zink	0,999 988
Aluminium	1,000 022 0	Silber	0,999 981
Platin	1,000 360	Quecksilber	0,999 975

Die Magnetfeld verstärkende Eigenschaft ferromomagnetischer Werkstoffe beruht auf die im Material vorhandenen Kristallbereiche, in denen die Rotationsachsen einiger Elektronen die gleiche Lage besitzen und somit als Gruppe wie kleine Dauermagnete wirken. Im unmagnetischen Zustand sind diese als Weißsche Bezirke bekannten Bereiche ungeordnet und treten nach außen nicht in Erscheinung (Bild 32, links). Unter dem Einfluss eines äußeren Magnetfeldes werden diese Elementarmagnete jedoch geordnet. Sind alle Elementarmagnete ausgerichtet, so ist das Material magnetisch gesättigt und zu einem Magneten geworden (Bild 32, rechts).

In einem Video von Eberhard Karls (Universität Tübingen) wird sehr anschaulich der Effekt der magnetischen Hysterese beschrieben (https://www.youtube.com/watch?v=Kp5PuUFv-4I).

Mit der Ausrichtung der Elementarmagnete in den Weißschen Bezirken wird auch der nichtlineare Verlauf der Magnetisierungskennlinie ferromagnetischer Werkstoffe verständlich. In Bild 33 sind dazu die Magnetisierungskennlinien von Elektroblech, Stahlguss (Neukurve, dunkelrot) und Gusseisen (grün) dargestellt, wenn sie zuvor noch nicht magnetisiert waren. Zu Beginn der Magnetisierung muss die Feldstärke erst einen bestimmten Wert erreichen, damit das magnetische Moment zum Verschieben der Blochschen Wände und das Ausrichten der Elementarmagnete vorhanden ist. Solange das nicht der Fall ist, ist die Permeabilitätszahl sehr klein. Im nächsten Schritt beginnt die Ausrichtung der Elementarmagnete und die Permeabiltätszahl steigt stark an. Die Feldstärke, bei der die meisten Elementarmagnete gleichzeitig ausgerichtet werden, repräsentiert den Punkt der maximalen Steigung der Magnetisierungskennlinie bzw. den höchsten Wert der Permibilitätszahl. Für die wenigen am Ende noch übrigbleibenden unausgerichteten Elementarmagnete, ist eine relativ hohe Feldstärke erforderlich. Wenn alle Elementarmagnete ausgerichtet sind, steigt die magnetische Flussdichte nur noch sehr gering und linear mit zunehmender Feldstärke an – das Material ist magnetisch gesättigt und die Permeabiltätszahl sinkt auf einen sehr kleinen Wert. In der Praxis ist eine gute magnetische Leitfähigkeit gefordert, daher vermeidet man das Erreichen des Sättigungszustandes.

Wird ein ferromagnetischer Stoff vollständig magnetisiert (Neukurve in Bild 33) und danach die Feldstärke kontinuierlich auf Null verringert, so tritt eine materialspezifische Remanenz B_R (Restmagnetismus) auf. Die Remanenz ist im Bild 33 als blauer senkrechter Pfeil dargestellt. Es springen somit nicht alle Elementarmagnete wieder in ihre Ursprungslage zurück. Um dies zu erreichen, ist eine negative Feldstärke – die sogenannte Koerzitivfeldstärke H_C (blauer waagerechter Pfeil) – notwendig. Dazu muss das äußere magnetische Feld umgepolt werden. Eine weitere negative Erhöhung der Feldstärke richtet die Elementarmagnete des Materials in entgegengesetzter Richtung aus, bis die negative Sättigung erreicht wird. Ein Absenken der negativen Feldstärke bis auf den Wert Null führt erneut zu einer Remanenz, die nur mit Hilfe der positiven Koerzitivfeldstärke aufgehoben werden kann. Die weitere Erhöhung der positiven Feldstärke verursacht wieder eine positive Magnetisierung des Werkstoffes. Der dabei entstehende geschlossene Magnetisierungskennlinienverlauf wird als magnetische Hysterese bezeichnet.

Die Ausrichtung der Elementarmagnete im Material erfolgt nicht kontinuierlich, wie der Verlauf der Hysterese vermuten lässt, sondern schlagartig. Dies wird erkennbar, wenn ein kleiner Teil der Hysterese stark vergrößert wird (Quadrat in Bild 33). Die plötzliche gleichzeitige Ausrichtung der Elementarmagnete in den Weiss’schen Bezirken wird Barkhausen-Effekt oder auch Barkhausen-Sprünge genannt. Mit den Sprüngen ist eine impulsartige kleine Stromänderung in der Spule verbunden, die über einen Verstärker hörbar gemacht werden kann.

Wie bei einem elektrischen Leiter, dessen Leitwert vom Material, der Leiterlänge und dem Querschnitt abhängt, lässt sich auch für den magnetischen Kreis ein magnetischer Leitwert berechnen. Besonders einfach wird die Berechnung des Leitwertes, wenn es sich um ein homogenes und auf einen definierten räumlichen Bereich beschränktes magnetisches Feld handelt. Fließt ein Strom durch einen Spulendraht, der lediglich einmal (N = 1) um einen geschlossenen Eisenkern gewickelt wurde, so verlaufen die meisten Feldlinien im räumlich begrenzten Kernmaterial. Im Bild 34 ist das Magnetfeld innerhalb eines aus einer Eisenlegierung bestehenden Schnittbandkerns zu sehen, auf dem sich eine Windung befindet.

Für die im Kern verlaufenden Feldlinien lässt sich die mittlere Feldlinienlänge l_m über die Kernabmessungen bestimmen. Die Querschnittsfläche A ergibt sich aus dem Produkt der Kantenlängen und die materialspezifische Permeabilität kann mit Hilfe der Magnetisierungskennlinie des Herstellers für eine bestimmte Feldstärke H über die Gleichung der magnetischen Flussdichte B {7.2.8} berechnet werden. Die Abmessungen des Eisenkernes beeinflussen somit unmittelbar den magnetischen Leitwert. Dieser steigt (in Analogie zum Leitwert eines elektrischen Leiters) mit höherer magnetischer Leitfähigkeit des Materials, bei Abnahme der mittleren Feldlinienlänge und bei Vergößerung des Querschnittes.

In Abhängigkeit der magnetischen Flussdichte B und dem magnetischen Widerstand R_m bzw. Leitwert Λ, bildet sich innerhalb des in der Spule befindlichen Werkstoffes, ein magnetischer Fluss Φ (Phi) aus (siehe Bild 34). Dieser ist vergleichbar mit dem elektrischen Strom durch einen Leiterwiderstand. Der magnetische Fluss repräsentiert die Gesamtzahl aller auftretenden Feldlinien und somit die Höhe des „magnetischen Stromes“. Ein größerer Querschnitt A des Werkstoffes bzw. des Hohlraumes senkt den magnetischen Widerstand R_m und führt zu einem höheren magnetischen Fluss. Wird die magnetische Flussdichte B erhöht (größerer Strom, höhere Windungszahl, Kernmaterial mit höherer Permeabilität), so führt auch das zu einem proportionalen Anstieg des magnetischen Flusses Φ.

In Bild 35 wird die Analogie zwischen dem elektrischen Stromkreis und dem magnetischen Kreis mit Hilfe der dazugehörigen Größen verdeutlicht.

Die Spannungsquelle U des elektrischen Stromkreises lässt sich aus in Reihe geschalteten Primärzellen (U₀) zusammensetzen. Im magnetischen Kreis ist die magnetische Durchflutung Θ die „Spannungsquelle“. Die Durchflutung steigt mit der Größe des Stromes und der Zahl der Windungen.

Nachfolgend sind die Zusammenhänge der beiden Kreise in tabellarischer Form zusammengefasst.

	Elektrischer Stromkreis	Magnetischer Kreis
Ursache	Elektrische Spannung U	Magnetische Durchflutung (Magnetische Spannung)
Widerstand	Elektrischer Widerstand der Leitung	Widerstand des magnetischen Kreises
Wirkung	Elektrischer Strom Ohmsches Gesetz (OG) Stromdichte	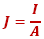Magnetischer Fluss OG magnetischer Kreis Magnetische Flussdichte (Magnetische Induktion)

 

 

7.2.6 Das Induktionsgesetz der Ruhe (Transformatorprinzip)

Seit der Zeit als Hans Christian Ørsted den Elektromagnetismus als zweiter entdeckte und Joseph Henry mit seinen Eisenkern-Spulen immer stärkere magnetische Flüsse erzeugte, wurde durch Experimente versucht, den umgekehrten Weg zu beschreiten und aus dem magnetischen Fluss wieder einen Strom zu gewinnen. Es vergingen viele Jahre bis Michael Faraday (1791–1867) im Jahr 1831 die Umkehrung dieses Prinzips – die elektromagnetische Induktion – entdeckte.

Dazu verwendete Faraday den in Bild 36 dargestellten Versuchsaufbau. Er wickelte auf einen Eisenring zwei Drahtwicklungen. Die erste Wicklung schloss er über einen Schalter an eine Batterie an. Die zweite verband er mit einem Galvanometer, mit dem er den fließenden Strom in der zweiten Wicklung nachwies.

Jedesmal, wenn er den Schalter schloss oder öffnete, stellte er fest, dass die Kompassnadel seines Galvanometers ausschlug. Änderte sich der Strom nicht, blieb die Kompassnadel in ihrer Ruhelage.

 

Das Schließen und Öffnen des Schalters führt zu einer sehr schnellen Stromänderung ΔI im Primärstromkreis und, da der magnetische Fluss dem Strom direkt proportional ist, zu einer schlagartigen magnetischen Flussänderung ΔΦ. Diese Flussänderung induziert in der zweiten Wicklung kurzzeitig eine elektrische Spannung U_i, die den Strom I_i durch den Sekundärstromkreis treibt. Bei einer positiven Änderung des magnetischen Flusses (Einschaltvorgang, blaue Pfeile) schlägt die Kompassnadel des Galvanometers zur rechten Seite (Bild 36) und bei einer negativen Flussänderung (Ausschaltvorgang, violette Pfeile) zur linken Seite aus. Die Polarität der erzeugten Spannung und die daraus resultierende Stromrichtung ist somit davon abhängig, ob der magnetische Fluss steigt oder sinkt.

Die Größe der induzierten Spannung U_i wird durch die Änderungsgeschwindigkeit des magnetischen Flusses, d. h. dem Quotienten aus der Höhe der Änderung ΔΦ und der Zeit Δt, in der diese Änderung erfolgt, bestimmt. Außerdem steigt die Indukrionsspannung linear mit der Windungszahl N.

Mit der Entdeckung der elektromagnetischen Induktion wurde es möglich, die elektrische Energie von einem Stromkreis (Primärkreis) mit Hilfe eines magnetischen Feldes über eine räumliche Distanz zu einem zweiten Stromkreis (Sekundärkreis) zu übertragen. Als Energieübertragungsmedium fungiert der Eisenkern, über den die magnetische Energie in gebündelter Form dem Sekundärkreis zugeführt wird. Da beide Stromkreise elektrisch voneinander isoliert sind, spricht man in diesem Zusammenhang von einer galvanischen Trennung.

Die Übertragung der elektrischen Energie erfolgt über zwei Energie-Transformationen (elektrisch → magnetisch, magnetisch → elektrisch), die mit Übertragungsverlusten verbunden sind. Das in Bild 36 dargestellte Übertragungskonstrukt wird daher in der Energietechnik Transformator und in der Audiotechnik Übertrager genannt. Für eine Dauer-Transformation ist eine permanente Änderung des magnetischen Flusses erforderlich. In der Praxis wird der Primärkreis daher mit einer Wechselspannung gespeist. Der Transformator gehört somit zu den Wechselstrombauelementen. Seine technischen Eigenschaften werden ausführlich im Lernmodul „Wechselstromtechnik“ beschrieben.

 

7.2.7 Die Selbstinduktion und Induktivität

Im vorletzten Abschnitt wurde aus den magnetischen Grundgrößen der magnetische Leitwert Λ bzw. Widerstand R_m abgeleitet (Gleichung {7.2.9} bzw. {7.2.12}). Diese konstanten Spulenparameter gelten nur für eine Spule mit einer Windung (N = 1). Eine Spule besitzt aber meist sehr viele Windungen, die in der Regel auf einen gemeinsamen Kern gewickelt und in Serie geschaltet sind. Beim Zuschalten der Versorgungsspannung springt der Strom zunächst von Null auf einen konstanten Wert, der in allen Windungen gleich groß ist. Jede Windung wird im Einschaltaugenblick vom eigenen Magnetfeld und der Summe der Magnetfelder der anderen Windungen durchsetzt. Es kommt somit zu einer magnetischen Kopplung der Einzelfelder, die wir bereits als magnetische Durchflutung Θ = I·N oder – in Analogie zum elektrischen Stromkreis – als magnetische Spannung kennnen gelernt haben. Die sprunghafte Einschalt-Stromänderung ΔI verursacht gleichzeitig eine Änderung der magnetischen Durchflutung ΔΘ = ΔI·N und – da der magnetische Widerstand R_m konstant ist – eine Änderung des magnetischen Flusses ΔΦ. Damit entsteht nach dem Induktionsgesetz in der Spule eine Selbstinduktionsspannung U_i.

Ausgehend von der allgemeinen Gleichung für die Induktionsspannung in einer Spule {7.2.17}, ersetzen wir die Änderung des magnetischen Flusses ΔΦ durch die Gleichung für das ohmsche Gesetz des magnetischen Kreises.

Im nächsten Schritt wird die magnetische Durchflutung ΔΘ ersetzt.

Die Windungszahl tritt in dieser Gleichung nun zweimal auf und wird als Potenz zusammengefasst.

Das Ergebnis zeigt, dass die Windungszahl maßgeblich die Höhe der Induktionsspannung beeinflusst, da sie quadratisch in die Gleichung eingeht. Einmal direkt und ein zweites Mal indirekt über die magnetischen Durchflutung ΔΘ. Statt der Änderungsgeschwindigkeit des magnetischen Flusses enthält die Gleichung nun die Änderungsgeschwindigkeit des Stromes. Dies ist in der Praxis von Vorteil, da die Stromänderung ΔI im Vergleich zur magnetischen Flussänderung ΔΦ messtechnisch einfacher ermittelt werden kann. Der rote Faktor vor der Änderungsgeschwindigkeit des Stromes kennzeichnet die konstruktiven Eigenschaften der Spule. Er wird Selbstinduktionskoeffizient oder Induktivität genannt.

 

7.2.8 Einschaltvorgang

Es soll nun die Auswirkung der Selbstinduktionsspannung beim Einschalten des in Bild 37 dargestellten Stromkreises untersucht werden. In der Schaltung sind zwei Glühlampen parallel geschaltet. Zur zweiten Glühlampe ist eine Spule mit der Induktivität von L = 10 mH und einem Wicklungswiderstand von R_L = 15 Ω in Serie geschaltet. Die Induktivität und der Wicklungswiderstand der realen Spule bilden eine untrennbare Einheit. Dies wird in der Schaltung durch Einrahmung und farbliche Hinterlegung hervorgehoben.

Aufgrund des Wicklungswiderstandes kann im Strang nicht der maximale Glühlampenstrom von 40 mA fließen. Die Helligkeit der Glühlampe wird daher etwas geringer sein. Es ist aber gewünscht, dass beide Glühlampen gleich hell leuchten. Um dies zu gewährleisten, wird auch zur ersten Glühlampe ein 15 Ω-Widerstand in Serie geschaltet.

Nach dem Zuschalten der Versorgungsspannung leuchtet die erste Glühlampe P1 sofort und die zweite Glühlampe P2 erst nach einer zeitlichen Verzögerung. Beim Einschalten wird der Stromfluss durch die zweite Glühlampe zunächst gehemmt. In der Spulenwicklung muss daher eine Selbstinduktionsspannung erzeugt werden, die der angelegten Spannung im Einschaltmoment entgegenwirkt.

 

Im Bild 38 ist das Ersatzschaltbild der Induktivität im Einschaltaugenblick dargestellt. Die Spule wirkt aufgrund ihrer selbstinduzierten Spannung als Gleichspannungsquelle. Da sowohl die Beträge als auch die Polarität der induzierten und angelegten Spannung identisch sind, kompensieren sich beide Spannungen zu Null. Es scheint so, als hätte die Induktivität einen unendlich großen Widerstand, was einer Unterbrechung des Stromkreises im Innern der Induktivität L entspricht. Im zweiten Lampenstrang kann daher kein Strom fließen und die Lampe bleibt zunächst dunkel. Mit der Zeit verringert sich die Selbstinduktionsspannung, bis sie den Wert Null erreicht. Parallel dazu steigt der Strom I₂ bis zu seinem Maximalwert. Die Glühlampe brennt mit maximaler Helligkeit.

 

An dieser Stelle sollen die zeitlichen Verläufe von Strom und Spannung an der Spule beim Einschalten untersucht werden. Für die allgemeine Betrachtung empfielt es sich, von einer idealen Spule (R_L = 0 Ω) auszugehen. In der Praxis gibt es eine Spule mit dem Widerstand 0 Ω nur, wenn der Wicklungsdraht supraleitfähig ist. Der Wicklungswiderstand R_L kann aber auch vernachlässigt werden, wenn ein im Stromkreis vorhandener Serienwiderstand wesentlich größer als der Wicklungswiderstand der Spule ist. Damit diese Voraussetzung bei der verwendeten Spule mit R_L = 15 Ω erfüllt ist, wird ein Widerstand von R = 2,7 kΩ in Serie geschaltet (Bild 39).

Nach dem Schließen des Schalters fließt in der RL-Serienschaltung kurzzeitig ein Strom I_L0, dessen Größe die Stärke des sich aufbauenden Magnetfeldes beeinflusst. Er beträgt …

Der Aufbau des Magnetfeldes verursacht eine Änderung des magnetischen Flusses. Dieser wiederum erzeugt die Selbstinduktionsspannung …

Da der Strom zuvor Null war, ergibt sich als Stromdifferenz der Wert I_L0. Die Gleichung für den Strom I_L0 wird in die letzte Gleichung eingesetzt …

Im Einschaltmoment ist die Selbstinduktionsspannung der Spule und die Versorgungsspannung gleich groß; es gilt daher …

Damit darf U_L0 durch U in unserer Gleichung ersetzt werden.

Die Spannung U lässt sich durch Division mit U aus der Gleichung herauskürzen.

Die Multiplikation der Gleichung mit t liefert eine für den Einschaltvorgang bedeutsame – von Induktivität und Spulenwiderstand abhängige – konstante Zeitgröße.

Wie beim Kondensator wird das t dieser Zeitkonstante durch den griechischen Buchstaben τ (Tau) ersetzt.

In der Spule kann die zugeführte elektrische Energie nicht schlagartig in ein magnetisches Feld umgewandelt werden. Im Einschaltmoment springt der Strom kurzzeitig von Null auf seinen Maximalwert. Die Stromänderung beträgt:

Die mit der Stromänderung einhergehende Änderung des magnetischen Flusses erzeugt eine Selbstinduktionsspannung in Höhe der Versorgungsspannung, die die Transformation sofort hemmt und den Stromfluss kurzzeitig beendet. Für die Aufrechterhaltung der Selbstinduktionsspannung ist aber eine Stromänderung notwendig, die sich erst wieder einstellen kann, wenn sich die Selbstinduktionsspannung verringert. Die Spannung bricht daher sehr schnell zusammen und der Strom steigt erneut an, wodurch wieder eine Selbstinduktionsspannung entsteht. Während dieses Wechselspiels steht aber immer weniger elektrische Energie zur Verfügung, da die sich um die Spule ausbildende magnetische Feldenergie mit jedem Stromanstieg vergrößert. Dadurch sinkt der Betrag der Flussänderung ΔΦ und die Selbstinduktionsspannung der Spule nimmt immer mehr ab, bis sie den Wert Null erreicht. Gleichzeitig steigt der Strom bis zu seinem Maximalwert I_L0 an. Die Zeitkonstante τ bestimmt die Geschwindigkeit mit der sich die Selbstinduktionsspannung vermindert und somit auch die Geschwindigkeit, mit der der Strom zunimmt. Dies wird auch aus der nach dem zeitabhängigen Strom I(t) umgestellten Maschengleichung für den Stromkreis in Bild 39 ersichtlich.

Wie bereits beim Kondensator, haben auch bei der Spule Strom und Spannung im Einschaltmoment einen charakteristischen zeitlichen Verlauf, der sich mit Hilfe der natürlichen Exponentialfunktion (e-Funktion) mathematisch beschreiben lässt.

In Bild 40 ist der normierte Stromverlauf und in Bild 41 der normierte Spannungsverlauf an der Spule dargestellt. Die eingezeichneten Prozentwerte ergeben sich, wenn in die normierten Gleichungen für den Spulenstrom und der Spulenspannung für die Zeit der Wert von τ bzw. die ganzzahligen Vielfachen der Zeitkonstanten eingesetzt werden (siehe 7.1.4 Lade- und Endladevorgang am Kondensator).

Der Strom ist nach der Zeit τ = R·C auf ca. 63 % seines Maximalwertes I_L0 angestiegen. Die Spannung hingegen auf 37 % ihres Maximalwertes U gesunken. Nach der Zeit t = 2τ ist der Strom nochmals um 63 % der noch verbleibenden Differenz zwischen dem Stromwert bei t = τ und dem Maximalwert I_L0 gestiegen. Er erreicht somit 86 % seines Maximalwertes. Die Spannung fällt dagegen um weitere 63 % – also auf 14 % des Maximalwertes – ab. Das Ganze wiederholt sich für die weiteren Zeitpunkte der ganzzahligen Vielfache der Zeitkonstante.

Die in Bild 40 und 41 eingezeichneten gestrichelten Geraden kennzeichnen den jeweiligen Strom- bzw. Spannungsanstieg (die Steigungen) zu den Zeitpunkten t = 0 s, t = τ, t = 2τ, t = 3τ, t = 4τ und t = 5τ. Die (positive) Steigung des Stromanstiegs bzw. die (negative) Steigung des Spannungsabfalls wird mit der Zeit immer geringer. Für den vollständigen Aufbau des Magnetfeldes wird annähernd eine Zeit von t = 5τ benötigt.

 

Der Spannung am Widerstand R steigt nach der e-Funktion des Stromes, da der Strom am konstanten Widerstand einen dazu proportionalen Spannungsfall verursacht. Bild 42 zeigt den Spannungsverlauf am Widerstand in der nicht normierten Darstellung.

 

7.2.9 Ausschaltvorgang

Das Verhalten von Strom und Spannung beim Ausschalten eines Spulenstromkreises lässt sich sehr gut anhand der in Bild 43 dargestellten Experimentierschaltung zeigen. Parallel zur realen Spule ist eine Glimmlampe geschaltet, die eine Zündspannung von 90 V besitzt. In der Glimmlampe befindet sich ein Gasgemisch, welches – wie bei einer Leuchtstofflampe – erst bei Erreichen der Zündspannung eine Stoßionisation der Gasmoleküle und somit eine Lichtemission auslöst.

Bevor auf den Ausschaltvorgang im Detail eingegangen wird, soll zunächst die Zeit ermittelt werden, die nach dem Einschalten des Schalters vergehen muss, bevor der Ausschaltvorgang eingeleitet werden darf. Die Spule benötigt diese Zeit, um das Magnetfeld vollständig aufzubauen.

Der Innenwiderstand R_i der Spannungsquelle (9 V-Alkaline-Blockbatterie, ca. 2,5 Ω) ist nicht wesentlich kleiner als der Wicklungswiderstand R_L der Spule. Er hat einen Anteil von 14,3 % am Gesamtwiderstand (R_i + R_L) der Schaltung und darf deshalb bei der Berechnung der Zeitkonstante nicht vernachlässigt werden. Unter Berücksichtigung dieses Sachverhaltes, lassen sich die Zeitkonstante und die Gesamtzeit für den nahezu vollständigen Aufbau des Magnetfeldes wie folgt berechnen.

Die Zeit t ist sehr klein und der Spulenstrom I_L erreicht schnell seinen Maximalwert. Der Stromkreis kann unmittelbar nach dem Einschalten bedenkenlos wieder ausgeschaltet werden. Die Glimmlampe leuchtet beim Einschalten nicht, da die sich einstellende Spannung …

(Spannungsteilerregel!)

wesentlich geringer als die Zündspannung ist.

Beim Öffnen des Schalters lässt sich beobachten, dass die Glimmlampe kurz aufleuchtet. Die Spule erzeugt im Moment der Stromunterbrechung eine sehr hohe Spannung, die den Wert der Zündspannung weit überschreitet.

Im Ausschaltmoment springt der Strom schlagartig auf den Wert Null. Dadurch wird eine negative magnetische Flussänderung ΔΦ erzeugt, die eine Selbstinduktionsspannung verursacht, die den Strom in der ursprünglichen Höhe und Richtung weiter durch die Spule treibt. Obwohl sich durch das Ausschalten blitzartig der Gesamtwiderstand der Schaltung verändert, kann sich der Wert des Stromes zunächst nicht ändern.

 

Um die Größenänderung des Gesamtwiderstandes zu ermitteln, betrachten wir die Kennlinie der Glimmlampe (Bild 44). Bis zu einer Spannung von 80 V fließt durch sie kein Strom. Sie hat einen sehr hohen Widerstand. Erst wenn die Spannung 90 V (Punkt A) erreicht wird, zündet die Glimmlampe. Die Spannung bricht dabei kurzzeitig auf einen Spannungswert von ca. 55 V zusammen und der Widerstand wird schlagartig geringer (Punkt B). Der damit verbundene starke Stromanstieg führt zur Zerstörung der Glimmlampe, wenn die Versorgungsspannung nach dem Zünden nicht reduziert wird. Aus diesem Grund müssen Glimmlampen mit einen Vorwiderstand betrieben werden, der den Strom auf den maximalen zulässigen Wert begrenzt (Punkt C) und einen Teil der Versorgungs-spannung aufnimmt.

 

Der hohe Widerstand der noch nicht gezündeten Glimmlampe beeinflusst somit maßgeblich das weitere Geschehen in unserem Stromkreis. Um dies zu verdeutlichen, ist das Ersatzschaltbild für den Moment des Ausschaltens in Bild 45 dargestellt.

Der kurz nach dem Ausschalten des Stromkreises weiter fließende Strom I_Laus stößt auf einen nahezu unendlichen Widerstand (offene Klemmen) der Glimmlampe und verursacht dort kurzzeitig eine extrem hohe Spannung, die die Glimmlampe zündet. Vergleichbar ist diese Situation mit dem ruckartigen Verschließen eines zuvor aufgedrehten Wasserhahns. Die vorhandene Bewegungsenergie des Wasserstroms wird schlagartig gestoppt und verursacht einen deutlich hörbaren Knall in der Wasserleitung.

Mit dem Zünden der Glimmlampe sinkt der Widerstand der Lampe stark ab. Die in der Spule gespeicherte Energie wird schnell abgebaut.

Damit fällt der Spannungswert an der Glimmlampe schnell unter die Brennspannung. Sie blitzt daher beim Ausschalten nur kurz auf. Der von der Spule generierte Strom, bewirkt an der Glimmlampe eine Richtungsumkehr der Spannung.

Die Höhe der entstehenden negativen Spulenspannung, die in voller Höhe an dem größten Widerstand in der Schaltung (Glimmlampe) abfällt, lässt sich mathematisch durch folgenden Ansatz leicht bestimmen:

Die Stromwege vor und nach dem Abschalten sind unterschiedlich. Kurz vor der Abschaltung bestimmen die Widerstände R_i und R_L die Höhe des Stromes.

Nach der Stromkreisunterbrechung treibt die entstehende Selbstinduktionsspannung der Spule dieser Strom kurzzeitig weiter durch den Wicklungswiderstand R_L und den sehr hohen Widerstand R_Gl der Glimmlampe. Er erzeugt an Ihnen die Spannung …

In die Gleichung wird der Ausdruck für I_Laus eingesetzt.

Da der Widerstand der Glimmlampe wesentlich größer als der Widerstand R_L ist, lässt sich die Gleichung vereinfachen.

Der Zusammenhang zeigt, dass die Höhe der entstehenden Spannung im Wesentlichen vom Widerstand der Glimmlampe abhängt. Beträgt dieser beispielsweise 10 MΩ, entsteht ein theoretischer Spannungswert von …

Bei der realen Spule liegt die Spannung aufgrund der vorhandenen kleinen Spulenkapazität weit unter diesem Wert, aber immer noch im kilo-Volt-Bereich. Die hohe Spannung kann nur impulsartig und in Verbindung mit einem sehr kleinen Strom auftreten, da eine Spule mit der Induktivität von 10 mH keine große magnetische Feldenergie speichern und somit bei der Umwandlung auch nur eine kleine elektrische Energiemenge abgeben kann. Allerdings kann die schlagartige Energieabgabe zu Schäden innerhalb einer elektronischen Schaltung führen. So werden Halbleiterbauelemente sehr leicht durch die entstehenden hohen Spannungen zerstört. Aber auch elektro-mechanische Bauelemente können beschädigt werden.

Wenn die Glimmlampe aus dem Stromkreis entfernt wird, bildet der öffnende Schalterkontakt im Augenblick des Ausschaltens den größten Widerstand im Stromkreis. Beim Öffnen des Schalters entsteht die Hochspannung zwischen den Kontakten (Bild 46). Da der Kontaktabstand zunächst sehr klein ist, wird die dazwischen liegende Luft ionisiert und es entsteht ein Lichtbogen, der die Kontaktflächen verbrennt. In Abhängigkeit des fließenden Stromes und der Induktivitäten im Stromkreis können die Kontakte sogar verschweißen und den Schalter damit unbrauchbar machen. Bei Schaltern, die große induktive Lasten oder hohe Spannungen schalten, wird daher mit allen Mitteln versucht, die Entstehung eines Lichtbogens zu verhindern.

 

 

Die hohen Ausschaltspannungen können mit folgenden Schaltungsmaßnahmen minimiert werden.

• Verringerung des Spulenstromes (vor dem Ausschalten)
• Kurzschließen der Spulenwicklung (beim Ausschalten)
• RC-Schaltung parallel zur Spulenwicklung
• Antiparallel geschaltete Diode (niederohmige Verbindung zwischen Spulenwicklungsanschlüssen beim Ausschalten)
• Varistor (spannungsabhängiger Widerstand) parallel zur Spulenwicklung

Der zeitliche Verlauf des Stromes und der Spannungen in den beiden zuletzt betrachteten Stromkreisen ist mathematisch schwer zu erfassen, weil der die Zeitkonstante bestimmende Gesamtwiderstand beim Ausschalten des Stromkreises keinen konstanten Wert hat. So ist der Widerstand der Glimmlampe stark von der an ihr liegenden Spannung abhängig. Das Gleiche gilt auch für den öffnenden Schalter. Zwischen seinen getrennten Kontakten bildet sich ein Lichtbogen, der – in Abhängigkeit der Höhe der entstehenden Induktionsspannung – bis zu mehreren Millimetern Kontaktabstand zunächst einen wegabhängigen Widerstand bildet und anschließend erlischt (R = ∞).

Um auch für den Ausschaltvorgang eine exakte Berechnung des zeitlichen Verlaufes von Strom und Spannungen vornehmen zu können, müssen beim Ausschalten konstante Widerstände wirken. Dies ist aber nur realisierbar, wenn keine mechanische Trennung des Stromkreises erfolgt. Die Alternative zur Trennung ist das Kurzschließen der Spule beim Ausschalten. Dies hat ebenfalls den Effekt, dass die Spannung an der Spule zusammenbricht. Beim Kurzschluss muss allerdings gewährleistet werden, dass die Spannungsquelle diesen Kurzschluss verträgt, also kurzschlussfest ist.

Als alternative Möglichkeit kann die RL-Schaltung mit einer pulsierenden Gleichspannung gespeist werden.

 

7.2.10 Spannungs- und Stromverlauf bei pulsierender Gleichspannung

Wird an die RL-Serienschaltung mit Hilfe eines Generators eine pulsierende Gleichspannung gelegt, die sich mit einer in Serie geschalteten Gleichspannungs- und Rechteckspannungsquelle erzeugen lässt, so wird der Stromkreis nie mechanisch unterbrochen, obwohl der Spannungswert zwischen 0 und 9 V periodisch hin- und herspringt (siehe auch 4.4.5 Spannungsarten).

In Bild 47 ist die Schaltung mit Spule und Serienwiderstand dargestellt. Die Spule kann als ideal angesehen werden, da der Wert des Widerstandes mit 1 kΩ wesentlich größer als der Wicklungswiderstand (R_L = 15 Ω) ist und die Zeitkonstante maßgeblich bestimmt.

Die Zeitkonstante für den Ein- und Ausschaltvorgang beträgt …

 

Da die Ströme und Spannungen ihre jeweiligen Endwerte erreichen sollen, wurde am Generator als Impulsdauer die Zeit t = 5·τ = 50 µs eingestellt.

In Bild 48 ist der zeitliche Verlauf des Stromes und der Spannungen unter Annahme einer idealen Spule (R_L = 0 Ω) dargestellt.

Der Strom I_L und die Spannung U_R haben den gleichen zeitlichen Verlauf, da eine Änderung des Stromes eine proportionale Spannungsänderung am 1 kΩ-Widerstand verursacht.

Die periodischen Sprünge der Generatorspannung bewirken in der Spule periodische Selbstinduktionsspannungen mit positiven oder negativen Betrag in Höhe des Maximalwertes der Generatorspannung. Für diese Augenblicke besitzt die Spule scheinbar einen sehr großen inneren Widerstand. Über den Zeitraum der Impulsdauer fällt an der Spule ein durchschnittlicher Spannungswert ab. Damit hat auch der Widerstand der Spule einen durchschnittlichen Wert. Dieser Wechselstrom-bedingte scheinbare Widerstand, ist der sich bei einer bestimmten Wechselspannung einstellende Blindwiderstand (Reaktanz) der Spule.

Obwohl der Wicklungswiderstand in Bezug auf die Zeitkonstante vernachlässigt wurde, darf nicht vergessen werden, dass dieser untrennbar mit der Induktivität L verbunden ist. Real fällt an der Spule immer eine kleine Spannung nach der Zeit t = 5 τ ab. Sie beträgt bezogen auf die obige Schaltung bei einem Wicklungswiderstand von R_L = 15 Ω:

Die Spannung am Widerstand kann somit die Generatorspannung von U = 9 V nicht erreichen. Der Maximalwert beträgt lediglich:

Als maximaler Strom ergibt sich:

 

7.2.11 Serienschaltung nicht gekoppelter Spulen

Die mathematischen Gesetzmäßigkeiten von zusammengeschalteten Induktivitäten gelten nur, wenn sich die Magnetfelder der einzelnen Spulen nicht gegenseitig beeinflussen, d. h. sie dürfen nicht magnetisch (z. B. über einen gemeinsamen Eisenkern) gekoppelt sein.

In der Serienschaltung von Spulen fließt durch beide Spulen der gleiche Strom. Eine Stromänderung wirkt somit in gleicher Weise auf beide Spulen und erzeugt in jeder Spule eine Selbstinduktionsspannung, die nur von der Höhe der Stromänderungsgeschwindigkeit ΔI/Δt und der jeweiligen Induktivität abhängig ist.

Im Einschaltmoment des Stromes teilt sich die Gesamtspannung im Verhältnis der Induktivitätswerte auf. Werden zwei in Serie geschaltete Induktivitäten zu einer Ersatzinduktivität zusammengefasst, so muss an dieser beim Einschalten die Gesamtspannung abfallen (Bild 49).

Mit der Maschenregel ergibt sich …

Mit der Gleichung {7.2.21} für die Selbstinduktionsspannung der Spule und der an jeder Stelle des Stromkreises gleichen Stromänderung ΔI ergibt sich …

Abschließend wird die Gleichung mit dem Kehrwert der Änderungsgeschwindigkeit des Stromes multipliziert.

 

7.2.12 Parallelschaltung nicht gekoppelter Spulen

Werden zwei Induktivitäten parallel geschaltet, so stellt sich im Moment des Einschaltens an jeder Induktivität eine Spannung in Höhe der Generatorspannung ein (Bild 50). Da sich der Gesamtstrom in der Parallelschaltung aus der Summe der Teilströme der einzelnen Induktivitäten ergibt, setzt sich die Änderung des Gesamtstromes aus den Änderungswerten der einzelnen Teilströme zusammen.

Mit der Knotenpunktregel ergibt sich …

Die Gleichung für die Selbstinduktionsspannung der Spule wird nach der Stromänderung ΔI umgestellt …

und für die einzelnen Spulenstromänderungen in die Knotenpunktregel eingesetzt. Da die Spannungen alle identisch sind, ergibt sich …

Zum Schluss wird die gesamte Gleichung durch (U · Δt) geteilt.

 

7.2.13 Kenngrößen der realen Spule

Die wichtigen Kenndaten der realen Spule sind:

• Die Toleranz der Induktivität,
• der Wicklungswiderstand der Spule,
• der Blindwiderstand der Spule (nur relevant bei Wechselstrom)
• die maximale Strombelastbarkeit (abhängig vom Querschnitt des Wickeldrahtes),
• die Spannungsfestigkeit, Nennspannung (max. erlaubte Spannung),
• die Verlustleistung, ausgedrückt durch den Verlustfaktor tan δ bzw. der Güte Q_L
  (bei Wechselstrom),
  tan δ = 0 → kein Spannungsfall, keine Verlustleistung
  tan δ > 0 → vorhandener Spannungsfall → Verlustleistung
• interne Streukapazitäten, die zu einer zeitlichen Verschiebung der inneren Spulenströme führen,
• der Temperaturbeiwert der Induktivität,
• die Wicklungskapazität bei hohen Frequenzen und
• die Ummagnetisierungs- und Wirbelstromverluste, wenn die Spule einen Eisenkern besitzt (bei Wechselstrom).

Die Verlustleistung ist die Energie, die zum Aufbau der magnetischen Feldenergie nicht verwendet werden kann, weil sie z. B. bei einer Luftspule in Form von Wärme über den Wicklungswiderstand an die Umgebung abgegeben wird.

Bei Verwendung eines Spulenkernes treten zusätzlich Wärmeverluste im leitfähigen Kernmaterial auf, wenn ein stetig wechselndes Magnetfeld in diesem Wirbelströme induziert. Um die Wirbelstromverluste klein zu halten, verwendet man Kerne aus voneinander isolierten dünnen Lamellen, Eisenpulverkerne mit isolierenden Bindemitteln oder Ferrite (feinkörnige schlecht leitende Metalloxide, die in beliebige Formen gepresst werden können und eine hohe Permeabilität besitzen). Auf diese Weise werden die „Leiter-Querschnitte“ im Kernmaterial stark verkleinert und somit der „Leiterwiderstand“ vergrößert. Die Wirbelstromverluste werden somit deutlich geringer.

Zu den Wärmeverlusten im Kern addiert sich noch die Energie, die für die Ummagnetisierung der Weißschen Bezirke im Kernmaterial erforderlich ist. Es wird daher in der Praxis immer zwischen den Kupferverlusten und Kernverlusten unterschieden. Die auftretenden Kernverluste müssen bei Wechselstrom immer berücksichtigt werden, während sie bei Gleichstrom in der Regel vernachlässigbar sind.

Daneben gibt es hohe Streuflüsse bei Luftspulen und wesentlich kleinere bei Spulen mit Kernmaterialien, die von der Kernform abhängig sind.

Auch bei axialen Festinduktivitäten, deren Aussehen dem von Festwiderständen ähnlich ist, werden die Induktivitätswerte nach IEC^* 62-1974 mit Hilfe von Farbringen angegeben. Zu berücksichtigen ist allerdings, dass der sich ergebende Zahlenwert für die Induktivität immer in „µH“ angegeben wird. So ergibt sich z. B. bei der Kombination der Farbringe orange, schwarz, orange und gold ein Induktivitätswert von 30·10³ µH = 30 mH mit einer Toleranz von ±5 %.

^*IEC → International Electrotechnical Commission

 

7.2.14 Praktische Einsatzmöglichkeiten

Die meisten Spulen kommen in der Nachrichtentechnik bzw. in der Wechselstromtechnik zum Einsatz. Es gibt aber auch eine Menge Gleichstrom-Anwendungsbereiche. Wir wollen uns in diesem Modul im Wesentlichen auf den Gleichstromeinsatz beschränken aber generell auch die Einsatzgebiete aufzeigen, in denen uns Spulen im alltäglichen Leben begegnen. Durch die letzte Forderung werden auch einige Beispiele für den Einsatz in Wechselstromkreisen genannt.

Grundsätzlich werden in der Elektrotechnik Spulen wesentlich weniger eingesetzt, da sich das induktive Verhalten, insbesondere bei der Signalspannungsformung, relativ einfach mit Kondensatoren und Widerständen (teilweise unter Nutzung aktiver verstärkender Bauelemente) realisieren lässt. Kondensatoren und Widerstände lassen sich wesentlich preiswerter herstellen und bieten darüberhinaus den Vorteil, dass sie in Halbleiterschaltkreisen leichter integrierbar sind.

Zunächst wurden die Spulen von Joseph Henry als Elektromagnete eingesetzt. Dies ist auch heute z. B. in der Stahl- oder Autoverwertungsindustrie der Fall. Das Prinzip des Elektromagnetismus wurde aber auch schon früh in der Nachrichtentechnik zur Wiederauffrischung von z. B. Morse-Signalen bei langen Übertragungsstrecken mit Hilfe von Relais verwendet (franz. relais → Schalteinrichtung, Zwischenstation). Beim Relais wirkt das Magnetfeld einer vom Strom durchflossenen Spule mit Eisenkern auf Schaltkontakte ein (Bild 51).

Beim Einschalten der Spulenwicklung entsteht ein Magnetfeld, dass den beweglichen Anker anzieht. Damit wird der magnetische Eisenkreis über den Spulenkern, dem Joch und dem Anker geschlossen und die magnetische Wirkung verstärkt. Es befindet sich nun zwischen Eisenkern und Anker kein Luftspalt mehr, der zuvor einen großen magnetischen Widerstand darstellte. Der Haltestrom für den Anker ist somit immer geringer als der Anzugsstrom, der den magnetischen Widerstand des Luftspaltes (kleinere Permeabilität) erst überwinden muss.

Über den Anker werden mechanisch Schaltkontakte betätigt. Im Bild 51 sind Kontakte zu sehen, die einen Stromkreis schließen.

Daneben gibt es Öffner- und Umschaltkontakte. Ein Relais kann mehrere Kontakte gleichzeitig schalten. Mit Relais lassen sich über kleine Spulenströme große Lasten schalten. Der Spulenstromkreis ist elektrisch von den Kontaktstromkreisen isoliert – also galvanisch getrennt. So können Relais beispielsweise über die Schnittstelle eines Computers angesteuert werden und elektrische Geräte ein- und auszuschalten (unter Beachtung der in Abschnitt {7.2.9} genannten Schutzmaßnahmen für den Ausschaltvorgang). Es ist allerdings darauf zu achten, dass die verwendete Schnittstelle den benötigten Anzugsstrom liefern kann.

Mit Relais wurden in den 1940er Jahren Computer gebaut. Konrad Zuse stellte 1943 den ersten programmgesteuerten elektromechanischen Digitalrechner Z3 vor, der seine Berechnungen mit Hilfe von Relais ausführte.

Nach dem Prinzip des Relais werden auch heute noch elektromechanische Steuerungen realisiert, die mit Automatisierungseinrichtungen (Speicherprogrammierbare Steuerungen → SPS) aufgrund hoher Schaltleistungen nicht aufgebaut werden können oder aus Sicherheitsgründen (z. B. Notaus-Stromkreise) nicht aufgebaut werden dürfen. Ein „Relais“ für hohe Schaltleistungen wird „Schütz“ genannt und besitzt im Vergleich zum Relais eine Funkenlöschkammer, die einen entstehenden Lichtbogen beim Ein- bzw. Ausschalten großer Lasten sofort eliminiert. Zudem gibt es beim Schütz statt eines Klappankers einen Zuganker, der eine größere (deutlich hörbare) mechanische Schaltkraft bewirkt und lediglich Öffner- oder Schließerkontakte betätigt. Diese Kontakte sind zudem doppelt unterbrechend bzw. schließend (Bild 52).

Bei den diversen Ausführungen von Schützen, lassen sich die internen Spulen mit unterschiedlichen Betriebsspannungen ansteuern. So gibt es Schütze für 12 V, 24 V, 48 V, 110 V, 230 V oder 400 V für Gleich- und Wechselspannungen. Will man flexibler sein, verwendet man Schütze, die für einen Spannungsbereich (z. B. 100 V - 250 V oder 250 V - 500 V) ausgelegt sind und sowohl mit Gleich- als auch mit Wechselspannung betrieben werden können.

 

Wie bereits in Abschnitt {7.2.5} erwähnt, sorgt das Spulenmagnetfeld einer Luftspule dafür, dass ferromagnetische Werkstoffe mit großer Kraft in die Spule hineingezogen werden. Diese Eigenschaft wird bei Verriegelungsmagneten, Türöffner-Magneten, Summern oder Tür-Gongs genutzt. In Bild 53 ist ein Verriegelungsmagnet dargestellt, der beim Zuschalten der Spannung entriegelt.

Daneben gibt es Ausführungen, die beim Einschalten der Spannung verriegeln oder über eine Polaritätsänderung der Spannung bzw. über eine zweite Spule sowohl das Verriegeln als auch das Entriegeln ermöglichen. In der Automatisierungstechnik arbeiten zudem ziehende oder drückende Schaltventile für Flüssigkeiten und Gase nach dieser Technik.

Dieses Funktionsprinzip kann aber auch verwendet werden, um mechanische Schalter in die Ruhelage zu bringen. Ein Beispiel finden Sie in jedem Stromverteilerkasten. Die darin befindlichen Sicherungsautomaten, sogenannte LS-Schalter (LS → Leitungsschutz) enthalten Wechselstromspulen, die bei einem Kurzschluss den Stromkreis trennen.

Der in diesem Fall fließende hohe Strom erzeugt in einer Spule mit nur wenigen Windungen (aber großem Drahtquerschnitt!) ein Magnetfeld, welches einen Eisenstift anzieht und über eine Mechanik den LS-Schalter unterbricht (Bild 54).

Spulen finden sich in Gleich-, Wechselstrom- und Schrittmotoren. Sie sind dort so angeordnet, dass ein rotierendes Magnetfeld entsteht. Ein darin drehbar gelagerter Anker (Rotor), der aus einem Dauermagneten (Fahrraddynamo), einem Eisenkäfig (Käfigläufer, Asynchronmotor) oder einer Kombination aus Eisenkernen und Spulenwicklungen (Synchronmotor) bestehen kann, wird mit Hilfe des Magnetfeldes in Rotation versetzt. Es ist aber auch möglich, mit sehr wenigen Teilen einen kleinen (technisch nicht nutzbaren) Taschenmotor mit nur einer „Spulenwicklung“ und einem Permanentmagneten zu bauen.

 

Die Funken zum Zünden des Benzin-Luft-Gemisches in KFZ-Motoren werden mit Hilfe von Zündspulen erzeugt. Die Zündspule arbeitet nach dem Transformatorprinzip und besitzt zwei Wicklungen mit unterschiedlichen Windungszahlen und Drahtquerschnitten. Jeweils ein Ende der Primär- und Sekundärwicklung sind in der Zündspule miteinander verbunden. Es werden daher statt der üblichen vier Anschlüsse lediglich drei benötigt. Es handelt sich somit um eine Transformator-Sparschaltung (Bild 55).

Bei der Zündspule wird auf einen geschlossenen Eisenkern verzichtet, was den Vorteil hat, dass eine magnetische Sättigung des Kernmaterials nicht auftreten kann, weil der außerhalb der Spule auftretende magnetische Widerstand der Luft, die magnetische Flussdichte B vermindert und deren Abhängigkeit vom Strom linearisiert. Die Flussdichte steigt dadurch nahezu proportional mit der Größe des in der Primärwicklung fließenden Stromes.

Der Stromkreis der Primärwicklung wird in modernen Kraftfahrzeugen mit einem elektronischen Transistor-Leistungsschalter geschlossen und geöffnet. Um eine höhere Ausfallsicherheit zu gewährleisten, sitzt auf jeder Zündkerze ein Zündmodul mit eigener Zündspule.

In älteren Fahrzeugen gibt es nur eine Zündspule und einen mechanischen Unterbrecherkontakt, der über eine rotierende Nockenwelle im Zündverteiler den Stromkreis zur Primärwicklung schließt und öffnet. In Bild 56 ist das vereinfachte Zündsystem mit Unterbrecherkontakt (ohne Verteilerfinger) für die Funkenbildung an der Zündkerze eines Zylinders dargestellt.

Im linken Teil des Bildes ist der Unterbrecherkontakt zu sehen, der bei einer Umdrehung der rotierenden Welle viermal öffnet (4-Zylinder-Motor). Parallel zum Unterbrecherkontakt ist ein Kondensator mit hoher Spannungsfestigkeit geschaltet, der eine Funkenbildung am Unterbrecherkontakt verhindert und die Energieübertragung vom Primär- auf den Sekundärkreis optimiert.

Beim Schließen des Unterbrecherkontaktes wird aufgrund der Stromänderung eine Spannung in Höhe der Versorgungsspannung von 12 V in der Primärwicklung induziert. In der Zeit t = 5τ wird die zugeführte elektrische Energie nahezu vollständig in die magnetische Feldenergie umgewandelt.

Beim Öffnen des Unterbrecherkontaktes induziert der damit verbundene Zusammenbruch des magnetischen Feldes in der Primärwicklung der Zündspule eine Gleichspannung von ca. 300 V. Die Sekundärspule hat eine um den Faktor 100 größere Windungszahl. Damit ist nach Gleichung {7.2.17} auch die in ihr induzierte Spannung um den Faktor 100 größer als in der Primärwicklung. Sie beträgt ca. 30 000 V und erzeugt damit einen Zündfunken (Lichtbogen), der das Benzin-Luft-Gemisch zur Explosion bringt.

Nach dem Energieerhaltungssatz muss im Primär- und Sekundärkreis – unter Vernachlässigung der Verluste – immer die gleiche elektrische Leistung umgesetzt werden. Das Produkt P = U·I muss also konstant sein. Da die Spannung in der Sekundärwicklung um den Faktor 100 größer ist, ist der Strom um den Faktor 100 kleiner und es kann für die Wicklung ein kleinerer Drahtquerschnitt verwendet werden. Dies gilt im Übrigen für jeden Transformator.

Spulen werden in der Wechselstromtechnik auch zur Erzeugung der Zündspannung von Leuchtstofflampen eingesetzt, die – wie die bereits erwähnte Glimmlampe – zur Gruppe der Gasentladungslampen gehören. Da nach der Zündung der Strom einer Gasentladungslampe lawinenartig ansteigt und zu einer Zerstörung der Lampe führen würde, ist eine Strombegrenzung unbedingt erforderlich. Die Spule kann diese Funktion in Leuchtstofflampenschaltungen aufgrund ihres Wechselstromwiderstandes zusätzlich übernehmen. Da sie den Strom drosselt, bezeichnet man sie in derartigen Schaltungen auch als „Drossel“. In Bild 57 ist eine Animation der Leuchtstofflampenschaltung mit konventionellem Vorschaltgerät (Glimmstarter mit Bimetallkontakten) zu sehen. Jeder Bimetallkontakt besteht aus zwei übereinander liegenden Metallzungen verschiedener Materialien, die sich unter Temperatureinfluss unterschiedlich stark ausdehnen. Da beide Metallzungen fest miteinander verbunden sind, verbiegt sich der Bimetallkontakt bei Erwärmung. Die Kontakte befinden sich in einer kleinen Glimmlampe. Sie werden durch das leuchtende Gasgemisch beim Betrieb der Glimmlampe erwärmt, bis sie sich gegenseitig berühren.

Nach dem Einschalten des Netzschalters liegt an dem Glimmstarter eine Spannung, die größer als dessen Zündspannung ist – das Gas im Starter wird gezündet und leuchtet. Der Strom durch den Glimmstarter wird durch den Wechselstromwiderstand der Drossel begrenzt. Es fließt ein kleiner Strom über die Drossel, der linken Glühwendel, dem Glimmstarter und der rechten Glühwendel der Leuchtstofflampe. Im Glimmstarter erwärmen sich die Bimetallkontakte, bis sie sich berühren. Dadurch bricht die Spannung am Glimmstarter zusammen und die Glimmentladung wird unterbrochen. Es fließt nun ein hoher Strom und die Glühwendeln werden vorgeglüht. Sie emittieren freie Ladungsträger (Elektronen) in der nahen Umgebung der Glühwendeln. Dieses Vorglühen ermöglicht eine Zündung der Leuchtstofflampe mit einer kleineren Zündspannung. Die Bimetallkontakte kühlen sich ab und Öffnen den Stromkreis. In der Drossel wird dadurch eine Zündspannung von bis zu 1500 V erzeugt und die Leuchtstofflampe gezündet. Die Leitfähigkeit der Leuchtstofflampe nimmt schlagartig zu. Die Drossel begrenzt den Strom durch die Leuchtstofflampe, an der nach der Zündung eine Brennspannung anliegt, die kleiner als die Zündspannung des Glimmstarters ist. Auf diese Weise kann kein erneuter Startvorgang stattfinden. Gelingt die Zündung der Leuchtstofflampe nicht, liegt am Glimmstarter nach dem Öffnen der Bimetallkontakte wieder eine Spannung, die größer als die Zündspannung ist, die Glimmentladung erneut einleitet und die Bimetallkontakte ein zweites Mal erwärmt usw.

Neben den hier ausführlich beschriebenen Einsatzbereichen von Spulen finden sich Spulen in Lautsprechern. Durch sie fließt der Strom des Audiosignals und bewirkt in Kombination mit einem Permanentmagneten die Bewegung der Lautsprechermembran und somit die Erzeugung eines akustischen Signals. Das Umkehrprinzip (der Schall bewegt eine Membran, an der eine Spule befestigt ist, die sich im magnetischen Feld eines Permanentmagneten bewegt und eine Spannung erzeugt), wird bei einfachen Mikrofonen verwendet.

In der Automatisierungstechnik werden induktive Sensoren eingesetzt, um Objekte aus Eisen berührungslos zu erfassen. Diese Objekte bewirken eine Bündelung der ausgestrahlten Feldlinien und somit eine Vergrößerung der magnetischen Flussdichte. Die Auswertelektronik steuert dann entsprechende Schaltkontakte an.

Die Spule findet sich in Stromzangen, in denen das wechselnde magnetische Feld eines umklammerten Leiters in der Spule eine Spannung induziert, deren Größe eine Aussage über die Höhe des fließenden Stromes macht.

Spulen können aber auch zur Dämpfung von Störsignalen eingesetzt werden. Man verwendet dazu eine stromkompensierende Drossel oder Gleichtaktdrossel (CMC → common mode choke). Sie besitzt zwei gleiche Wicklungen, die gegensinnig vom Strom durchflossen werden. Dadurch heben sich die Magnetfelder im Kern gegenseitig auf und dämpfen die in der Regel gleichzeitig auf der Hin- und Rückleitung auftretenden Störsignale in einem Stromkreis.

 

---

Verwendete Quellen:
[5]	Wikipedia: Gian Domenico Romagnosi. http://upload.wikimedia.org/wikipedia/commons/d/d7/Romagnosi.jpg. Abrufdatum: 27.04.11
[6]	Smithsonian Institution Libraries (Galaxy of Images): Michael Faraday. http://www.sil.si.edu/imagegalaxy/imageGalaxy_enlarge.cfm?id_image=1004. Abrufdatum: 20.05.11
Weitere empfehlenswerte Literatur:
1.	Kurcz, F. (2010): Elektrische Bauelemente. http://www.kurcz.at/downloads/bauteile.pdf. Abrufdatum: 22.03.11
2.	Böhmer, E. (2004): Elemente der angewandten Elektronik. Wiesbaden: Vieweg & Sohn.
3.	Bieneck, W. (2005): Elektro T – Grundlagen der Elektrotechnik. Stuttgart: Holland + Josenhans.
4.	Lieberherr, M.: Theorieblatt „Magnetismus“. http://lie.perihel.ch/Theorieblaetter/Elektrizitaet/Einf_Magnetismus.pdf. Abrufdatum: 05.05.11
5.	Die HEA - Fachgemeinschaft für effiziente Energieanwendung e.V.: Joseph Henry, der Namensgeber der Induktivitätseinheit. http://www.hea.de/service/fachwissen/pioniere-der-elektronik/Joseph-Henry.php. Abrufdatum: 08.05.11
6.	Hermann, F.; Job, G.: Altlasten der Physik. Hallbergmoos: Aulis Verlag Deubner. Online abrufbar: http://www.physikdidaktik.uni-karlsruhe.de/altlast/index.html. Abrufdatum: 23.05.11
7.	Rötter, H. (Hrsg.) (2002): Kommunikationselektronik – Grundbildung. Haan-Gruiten: Europa-Lehrmittel.

 

---